Циркуляция магнитного поля по замкнутому контуру равна охватываемому им току
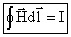
- магнитное поле - вихревое, порождается электрическими движущимися зарядами, его силовые линии всегда замкнуты, магнитных зарядов нет. Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического. Из теоремы Гаусса для векторного поля в дифференциальной форме следует, что поле можно представить в виде ротора вспомогательного векторного поля , называемого векторным потенциалом : 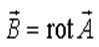
поскольку 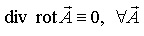 . Физический смысл в магнитостатике приписывают векторному полю , поэтому векторный потенциал, вообще говоря, определен с точностью до градиента любой скалярной функции. Действительно, если
. Физический смысл в магнитостатике приписывают векторному полю , поэтому векторный потенциал, вообще говоря, определен с точностью до градиента любой скалярной функции. Действительно, если 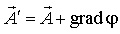 , где фи - скалярное поле, и
, где фи - скалярное поле, и 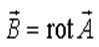 , то имеем:
, то имеем: 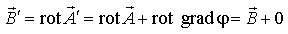
, то есть 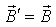 для
для 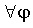 , поскольку
, поскольку 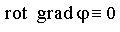 .
.
Циркуляция вектора магнитной индукции по замкнутому контуру , равна потоку вектора объемной плотности тока через произвольную поверхность , натянутую на этот контур, если направление обхода контура и направление нормали к поверхности согласованы между собой по правилу правого винта: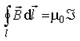
Возьмем контур l, охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции , т.е. .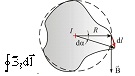
Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку (линии прямого тока – окружности). Воспользуемся свойствами скалярного произведения векторов.
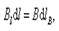 где – проекция dl на вектор , но , где R – расстояние от прямой тока I до dl.
где – проекция dl на вектор , но , где R – расстояние от прямой тока I до dl.
.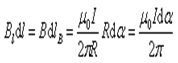
Отсюда
|
| , |
|
|
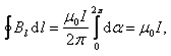 это теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.
это теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.
Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).
При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому  , и следовательно
, и следовательно 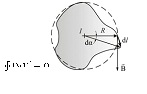
|
|
|
|
|
Итак, 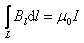 , где I – ток, охваченный контуром L.
, где I – ток, охваченный контуром L.
Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.
Если контур охватывает несколько токов, то 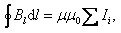
|
| , | (2.6.3) |
|
т.е. циркуляция вектора равна алгебраической сумме токов, охваченных контуром произвольной формы.
Теорема о циркуляции вектора индукции магнитного поля 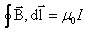 позволяет легко рассчитать величину В от бесконечного проводника с током: .
позволяет легко рассчитать величину В от бесконечного проводника с током: .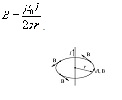
Итак, циркуляция вектора магнитной индукции B отлична от нуля, если контур охватывает ток (сравните с циркуляцией вектора E : 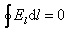 ).
).
Такие поля, называются вихревыми или соленоидальными. Магнитному полю нельзя приписывать потенциал, как электрическому полю. Этот потенциал не был бы однозначным: после каждого обхода по контуру он получал бы приращение .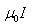
Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Линии всегда замкнуты. Поэтому теорема Гаусса для вектора магнитной индукции записывается так: 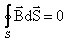
.